Érted a matekot kísérleti blog

Ebben a cikkben a négyszögekről, és a sokszögekről fog szó esni, egyébként ebben a sorrendben. Megnézzük milyen fajta sokszögek léteznek, és azoknak milyen tulajdonságaik vannak.

Négyszögek

A négyszögek négy darab szöggel rendelkező síkbeli testek. Ezzel azt hiszem senkinek nem árultam el újdonságot. 

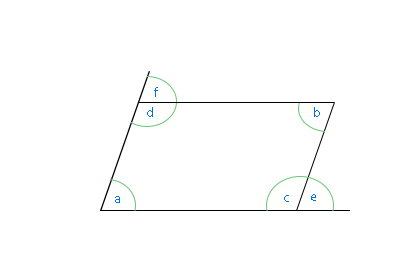
Kezdjük a paralelogrammával. A paralelogramma olyan négyszög, amelynek szemközti oldalai párhuzamosak.Az az érdekes vele kapcsolatban, hogy a szemben fekvő szögei egyenlőek. Nézzük erről egy ábrát. Az e és a b szögek egyenlők, mert váltószögek. Az a és az e szögek pedig egyállású szögek. Így nyilván a c és az a szögeknek is egyenlőnek kell lenniük. Az egy oldalon fekvő szögei pedig 180°-ra egészítik ki egymást. Az "a" és a "f" szögek egyállású szögek, és egyenlőek. A "d" és a "f" mellékszögek, tehát 180°-ot zárnak be együtt. Így az "a" és a "d" is 180°-os szöget alkotnak. 

A paralelogramma átlói felezik egymást. Az APB háromszög és a CPD háromszögek ugyan olyanok, ezt matematikául úgy mondjuk, hogy egybevágóak. Ha viszont ezek a háromszögek egybevágóak, akkor AP-PD szakad és a BP-PC szakasz egyenlő hosszúságúak. 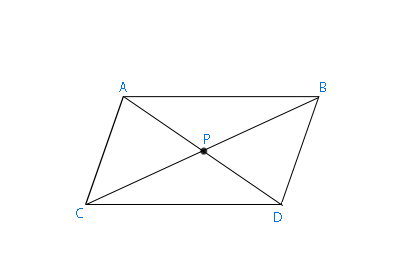A téglalap olyan paralelogramma, amelynek négy derékszöge van.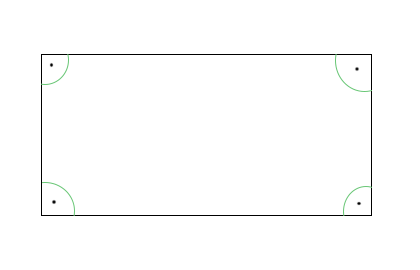
A rombusz olyan négyszög, amelynek szemben fekvő oldalai párhuzamosak, és az oldalai egyenlő hosszúságúak. Ha kicsit továbbgondoljuk, akkor arra a következtetésre jutunk, hogy a szemközti szögei ennek is egyenlő nagyságúak, illetve ezek átlói is felezik egymást. A rombusz esetében az átlók úgynevezett szimmetriatengelyek is. Ez nagyjából azt jelenti, hogy félbehajtanánk az átlók mentén, fednék egymást az így keletkezett háromszögek. Az átlók egyébként merőlegesek egymásra.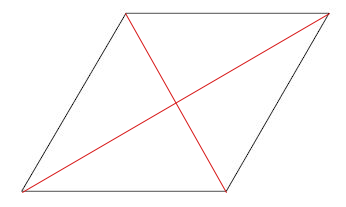 

A négyzetnek négy egyenlő oldala és négy derékszöge van. Ugyan az igaz rá, mint a rombuszra, csak ennek átlói megegyező hosszúságúak.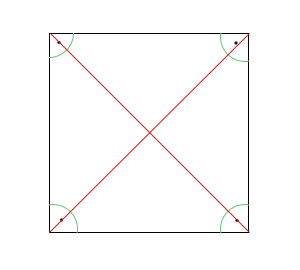 
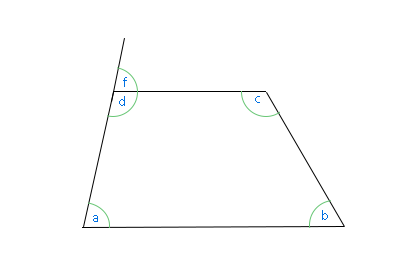
A trapéz olyan négyzet, melynek legalább két párhuzamos oldala van. Van egy speciális formája, mely a jobb oldalon látható, ezt derékszögű trapéznak nevezzük. Neki egy derékszöge van. A trapéz szemközti szögei 180 fokra egészítik ki egymást. Amint az alsó ábrán látjuk, az "a" és az "f" szögek egyenlők, a "d" és az "f" pedig egy egyenes szöget alkotnak. Így nyilván "a" és "d" is egyenes szöget kell, hogy létrehozzanak együtt.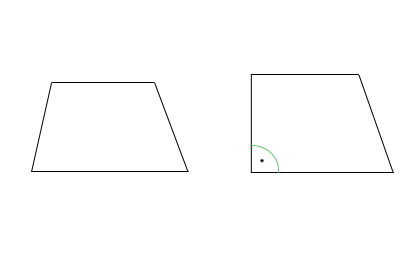Legvégül nézzük meg a deltoidod. A deltoid a papírsárkány forma. A deltoid átlói merőlegesek egymásra, és a hosszabbik átlója a deltoid szimmetriatengelye. (A szimmetriatengely mentén ha tükröznénk az egyik oldalt, ugyan azt az alakzatot kapnánk.)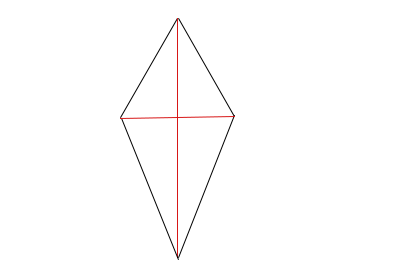 

A négyszög belső szögeinek összege 360°. A négyszöget átlói mentén két háromszögre bonthatjuk, egy háromszög belső szögeinek össze 180°.....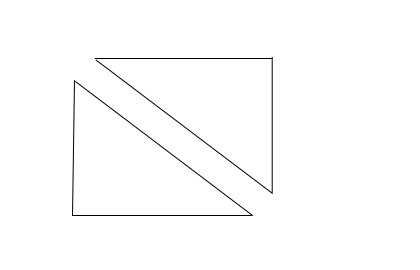

A sokszögek

Elég sokféle sokszög van, de bizonyos tulajdonságok mindegyikre egyaránt vonatkoznak. Ilyen például a sokszögek átlójának a száma. Ha meg akarjuk tudni egy százszög csúcsaiból hány átló húzható, akkor egy képletet kell segítségül hívnunk. Ez az [(n-3)*n]/2. (A * jel a szorzást jelenti.) De vajon hogyan áll össze ez a képlet? Ha az alsó ábrára tekintünk, akkor észrevesszük, hogy a sokszögek egy egy csúcsából átlók vanna húzva a szemközti csúcsba. Méghozzá annyi, amennyit egy átlóból maximálisan húzhatunk. Ez az ötszög esetében kettő, a hatszög esetében három, a hétszög esetében négy stb.... Ha n-et tekintjük a sokszög szögei számának, akkor mindig n-3. Tehát hárommal kevesebb, mint amennyi szöge van a síkidomnak. Ha viszont minden egyes csúcsból ennyi átló húzható, akkor nyilván az összes átlóból n-szer ennyi, tehát annyi, amennyi szöge van a sokszögnek. Ezzel csak annyi a probléma, hogyha az egyik csúcsból már húztunk egy átlót, és a vele szemben lévő csúcsból húzunk még egyet, akkor ugyan azt az átlót kapjuk. Tehát az n*(n-3)-at el kell osztani kettővel, hiszen minden csúccsal szemben elhelyezkedik egy másik csúcs. 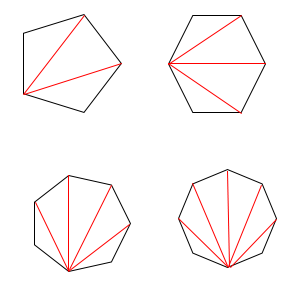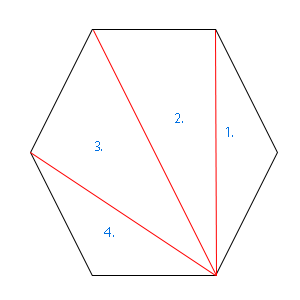Ha a háromszögnek 180° a négyszögnek 360° a belső szögeinek az összege, akkor mennyi mondjuk az hatszögnek?  az alsó képen egy szabályos hatszöget láthatunk, amit az átlóival háromszögekre bontottunk. Látható, hogy n-2, azaz négy háromszögre bonthatjuk ezt a síkidomot. Ez igaz bármelyik sokszögre. Mindig kettővel kevesebb háromszögre lehet bontani őket, mint ahány oldaluk van. Ha egy hatszög 4 db háromszögre bontható, akkor 4*180° a belső szögeinek összege. Jegyezzük meg ezt a képletet: (n-2)*180. 

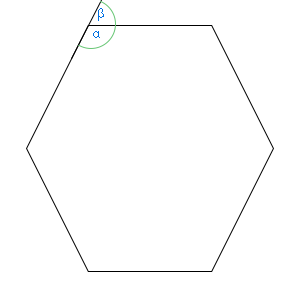
Ha a sokszög belső szögeinek összegét a fent vázolt módon kapjuk meg, akkor hogyan számolhatjuk ki a külső szögek összegét? Nézzük meg az alábbi hatszöget! Az alfa és a béta szögek mellékszögek, így 180°-ra egészítik ki egymást. Ez azt jelenti, hogy egy sokszög külső és belső szögeinek összege a sokszög szögeinek száma megszorozva 180°-kal. Nyilván, mert annyi külső szöge van a sokszögnek, ahány belső szöge. Ha ebből kivonjuk a belső szögeket, akkor megkapjuk a külső szögek nagyságát. Egy hatszög 6-2, azaz 4 háromszögre osztható szét. Tehát a belső szögeinek az összege 4*180, azaz 720°. A külső és belső szögek összege 6*180, azaz 1080°. 1080°-720°=360° 
Ez minden sokszögre igaz, a külső szögek összege 360°. 

Hogy számíthatjuk ki a sokszög középponti szögét? Egyáltalán mi az a középponti szög? Ha az alsó ábrára nézünk, akkor megtudjuk. Az alábbi hatszöget az hat darab háromszögre bontottuk. Ezt úgy értem el, hogy a csúcsokból a középpontba húztam szakaszokat. Egy egy ilyen háromszög belső csúcsának a szöge a középponti szög. Amint látható, egy kört lehet belerajzolni a hatszögbe. Ez azt jelenti, hogy az összes középponti szög összege 360°. Ha minden sokszöget annyi ilyen háromszögre tudunk bontani, mint ahány oldala van, akkor 360/n lesz a középponti szög nagysága. (Az n még mindig az oldalak vagy csúcsok száma.)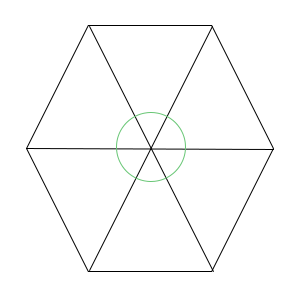
Nézzük meg mi az a belső szög, és az az egyes sokszögeknél mennyi! A belső szög az, amelyik nem a középponti. Mondhatnád, hogy de abból kettő van! Ez igaz, viszont mivel egyenlő oldalú háromszögekre bontottuk  a síkidomot, ezért a képen látható Υ és ß nagysága megegyezik. Tudjuk, hogy a háromszög belső szögeinek összege 180°. Ha alfa középponti szöget levonjuk a 180 fokból, akkor megkapjuk béta és gamma szöget. Mivel viszont ezek nagysága egyenlő, ezért simán elosztjuk kettővel, és megvan egyik és másik szög is. 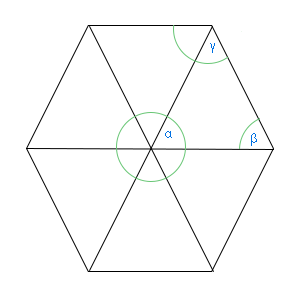Mekkora egy sokszög egyetlen külső szögének összege? Ha béta és gamma megegyezik, akkor gamma és gamma vessző is. Ha béta, gamma és alfa 180 fokos szöget alkotnak együtt, és gamma, gamma vessző és a külső szög is, akkor a külső és a középponti szög, és a külső szög egyforma nagyságúak. Tehát a sokszög külső szögeinek nagysága mindig megegyezik a sokszög középponti szögeinek nagyságával. Most nézzétek meg a négyzetről készült rajzokat />Itt egy paypal számla, amire tetszőleges összege utalhattok, ha hasznos volt számotokra az anyag: