A síkgeometria, síkbeli alakzatokkal foglalkozó tudományága a matematikának. Ebben a posztban a legalapvetőbb síkgeometria tételeket fogom kifejteni. Lehet, hogy sokaknak ez már ismerős lesz, és tudják, viszont én szükségesnek tartom leírni ezen alapfogalmakat.
Szögek
Hatféle szög létezik, ezek sorban a hegyesszög, derékszög, tompaszög, egyenesszög a homorú szög és a teljes szög.
Hegyesszög: 0°-90°-ig. Nyilván azért nevezik hegyesszögnek, mert hegyes.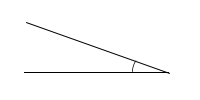 
A derékszög egy speciális, 90°-os szög. Így néz ki nagyjából:
A tompaszög olyan szög, mely 90°-nál nagyobb, de 180°-nál kisebb.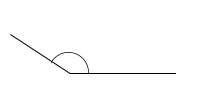 
Az egyenes szög éppen 180°-os. Tulajdonképpen egy egyenes.
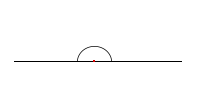A homorú szög 180°-nál nagyobb, de 360°-nál kisebb.
Végezetül a teljes szög éppen 360°-os, tehát egy teljes kört ír le.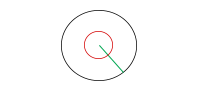 
A szögeket a görög ábécé betűivel jelöljük. Ha én nem így teszek, az azért van, mert lusta vagyok, és nincs kedvem paint-be különleges karaktereket importálni.
A háromszög
Most, hogy átismételtük milyen szögek léteznek, elemezzük egy kicsit az egyik legegyszerűbb síkgeometriai formát, a háromszöget. Ennél kevesebb szögű sokszögünk nem is igen lehet, viszont azért nem kéne csak úgy elsiklani felette. Szokták mondani, hogy a háromszög belső szögeinek összege 180°. De vajon miért van ez így? Nézzük meg a következő ábrát!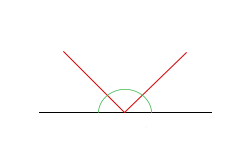
A két piros egyenes három darab szögre bontja a fekete szakaszunkat. A fekete szakasz értelmezhető egyenes szögként is. Ha belegondolunk, teljesen mindegy hogyan próbáljuk elosztani a teljes szöveg a piros szakaszokkal, mindenképpen 180° lenne az összegük. Most fordítsuk meg a két piros szakaszt!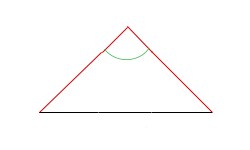 
Amint látható egy háromszöget kaptunk. Azt is észrevettük, hogyha a két másik szöggel ebben a formában akarjuk elosztani a fekete szakaszunkat, a fekete szakasznak mindenképpen egyenes szögnek kell lennie, ha mondjuk homorú szög lenne, akkor már nem három, hanem négy szöggel rendelkezne.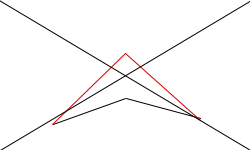 
Na ezért 180 º a háromszög belső szögeinek összege.
A háromszög csúcsait az ábécé nagy betűivel, a szögeit a görög ábécé betűivel, oldalait pedig az ábécé kis betűivel jelöljük.
Háromszögek típusai
A háromszöget oldalai, és szögei szerint lehet csoportosítani.
Oldalai szerint megkülönböztetünk szabályos háromszöget, melynek minden oldala egyenlő hosszúságú: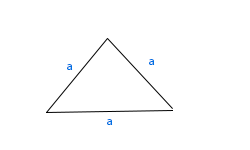
Egyenlő szárú háromszöget, melynek két szára egyenlő hosszúságú.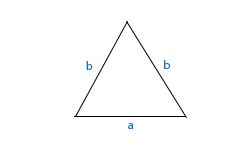 
Végezetül általános háromszöget, melynek nincsenek azonos méretű oldalai.
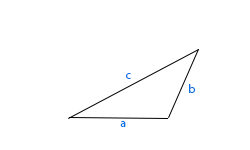
Szögei szerint megkülönböztetünk hegyesszögű, tompaszögű és derékszögű háromszöget.
A hegyesszögű háromszögnek három darab hegyesszöge van. Például ez is az:
A tompaszögű háromszögnek van egy darab tompaszöge.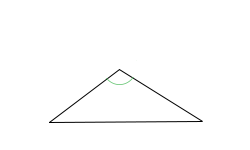 
A derékszögű háromszögnek pedig egy derékszöge van. (Szerintem nem kérdéses senki számára, hogy melyik a derékszög.)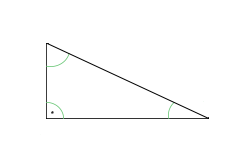 
Ajánlott bejegyzések:
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.