Tök jó, hogy az előző bejegyzésben megfogalmaztam, általában mit kell tudni a halmazokról, de a feladatok megoldása már más kérdés. Nézzünk egy egyszerű leckét!
Egy 225 fős társaságból 180-an kedvelik a Battlestar Galactica c. sorozatot, 120-an a Star Trek-et. 75 fő mindkét sorozatot kedveli. Egészítsd ki a Venn-diagramot! 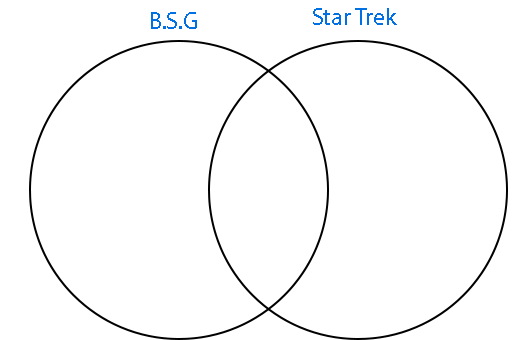
Az elég nyilvánvaló, hogy a két halmaz, és a metszeteiknek az összege nem haladhatja meg a 225-öt, hiszen 225 embert kérdeztünk meg. Vajon mit kell tenni, ha el akarjuk ezt érni? Először is a metszet részbe (a középső részbe) be kell írnunk azoknak az embereknek a számát, akik mindkét sorozatot szeretik. Ők 75-en vannak. Ha 180-an kedvelik a Battlestar Galactica-t, akkor vajon hányan vannak közülük, akik a BSG mellett a Star Treket is szeretik nézni? Azt állítottuk, hogy 180-an szeretik a BSG-t, nem azt, hogy csak azt szeretik. Nyilván 180-75-en előszeretettel bámulják a BSG-t, de csak azt. Azaz 105-en.
Ugyancsak ilyen eljárással kapjuk meg azoknak a számát, akik kizárólag a Star Treket hajlandók nézni a két sorozat közül. Tehét 120-75 azaz 45 főről van szó. Hogy néz ki most az ábra? 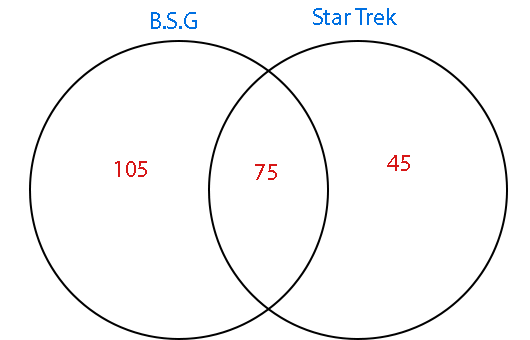
Ha összeadjuk a számokat, akkor kijön a 225 fő, tehát jól végeztük a dolgunkat. Most nézzünk egy kicsit bonyolultabb feladatot!
Egy iskolába 365 tanuló jár. Közülük 180-nak van táblagépe, 190 -nek okostelefonja, 200-nak pedig laptopja. Harminc diák mindhárom eszközzel rendelkezik. 75 tanuló tudhat magáénak táblagépet és okostelefont is, 85 okotelefont és laptopot, valamint 95 táblagépet és laptopot. Harminc diák mindhárom eszközzel rendelkezik. A harmincat be is írhatjuk a legbelső részbe. A kérdés az, vajon mennyi írjunk a közös részekbe? Azt mondtuk, 75 tanuló rendelkezik táblagéppel és okostelefonnal. Nyilván közülük harmincan mindhárom-féle eszközt birtokolják. Ez azt jelenti, hogy 75-ből le kell vonni 30-at, és így megkapjuk a táblagép és okostelefon közös részét, azaz a kettő metszetét. Viszont a 95 okosteló+laptopos és 95 táblagép+laptopos közül is rendelkeznek akár mindhárom eszközzel, így belőlük is le kell vonni azt a bizonyos harmincat. 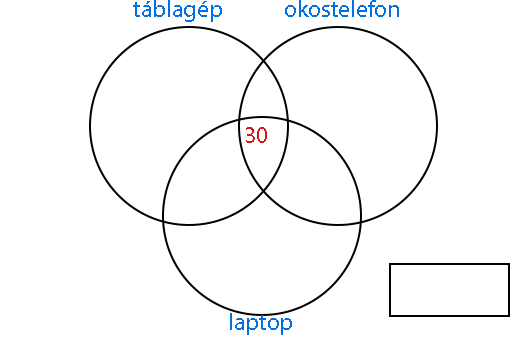
Hogy néz ki most az ábránk? A 75-ből, a 85-ből és a 95-ből is levontuk a 30-at. Így a következő eredményt kapjuk: 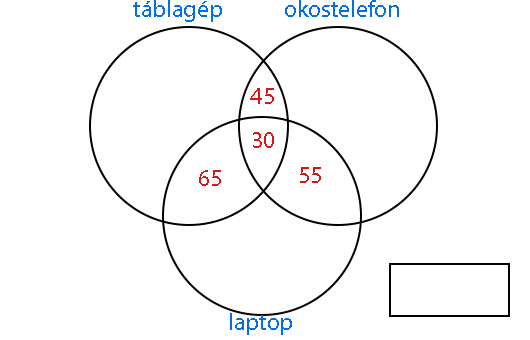
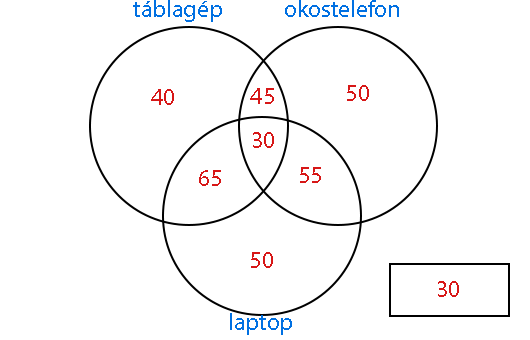
Felmerül a kérdés, vajon hányan lehetnek azok, akik csak az egyik vagy csak a másik eszközt tudhatják magukénak? Nyilván a 180 táblagépesből 45-nek van okostelefonja, 30-nak mindhárom eszköze, és 65-nek pedig laptopja is. Akkor egyértelmű, hogy ezeket az értékeket le kell vonni a 180-ból. Így marad 40. Ha azt kérdezzük, hogy hány nebulónak van csak okostelefonja a fent említett eszközök közül, akkor a választ megint hasonló eljárással kapjuk meg. Ki kell vonni azokat az okostelefon többi halmazzal alkotott metszeteit az összes okostelefonos közül. Így 60 lesz az eredmény. A laptopnál hasonló módszerrel pedig szintén 50. Ha összeszámoljuk az összes metszetben és halmazban lévő elemeket, akkor megkapjuk hány tanulónak van egyáltalán bármilyen eszköze a három közül. Így kapunk 335 diákot. Viszont nekünk 365 nebulónk volt eredetileg. A jobb oldalon alul elhelyezkedő kis téglalap a komplementer halmazunk, tehát azoknak a diákoknak a számát kell beírnunk, akiknek nincs se táblagépük, se laptopjuk, se okostelefonjuk.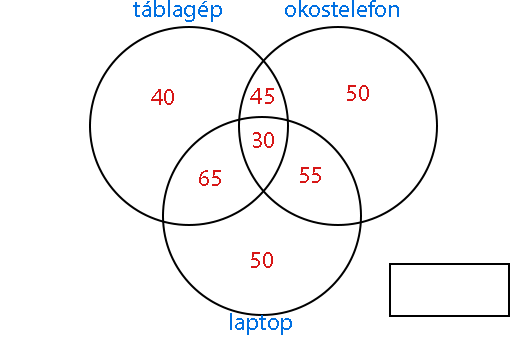
Ha hasznos volt számodra a bejegyzés, akkor nyomd meg az alsó gombot!
Itt egy paypal számla, amire tetszőleges összege utalhattok:


Ajánlott bejegyzések:
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.